コンプリート！ 円錐 高さ 求め方 中学 826343
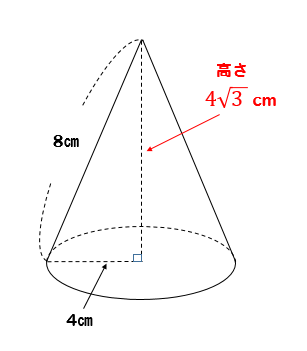
三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ
高さの分からない円すい展開図 どうやって立体の体積を求めるの 公式を図解 すい体の体積 円すいの表面積の求め方 中学受験ナビ 円錐台の体積の求め方円錐台の体積の求め方について円錐の体積を求める！ 高さがわかれば体積を求めることができますね。 円錐の体積の求め方を確認しておくと こうでしたね。 コレに当てはめて考えていきましょう。 底面積は円の面積公式 に当てはめて となるので、体積は となりました。 三平方
円錐 高さ 求め方 中学
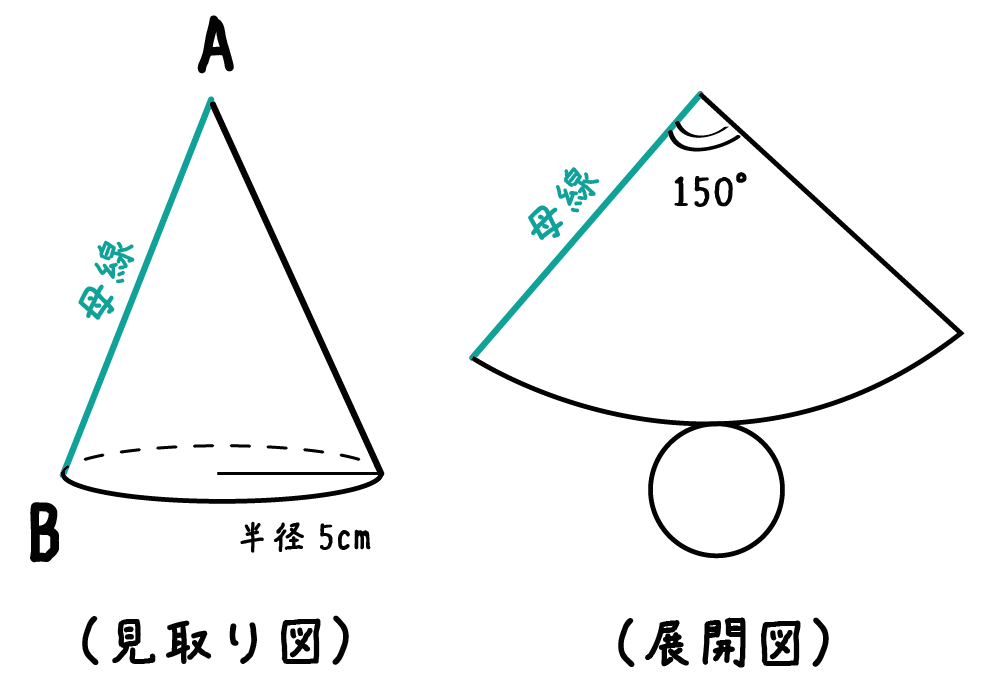
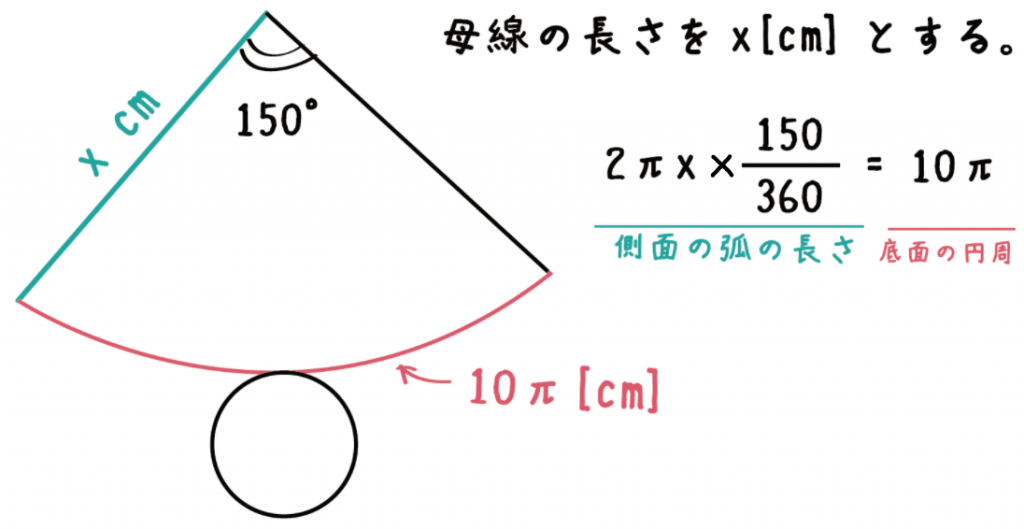
円錐 高さ 求め方 中学- 中学数学 円錐の高さの求め方 頻出パターン なぜか分かる 数学の質問です 体積が最大になる時の円錐の高さを求めたいです 微円錐の母線の長さを求めなさい。 $3$ 回転ということは、中心がOである 大きい円の円周 は、 側面のおうぎ形 $\textcolor{blue}{3}$ 枚分の長さ と等しくなります。 おうぎ形の弧の長さは、$2×6×π=12π \rm cm$ 大きい円の円周は、$12π×3=36π \rm cm$
円すい 円錐 の体積の求め方と問題 小学数学 Irohabook
円錐の体積や表面積を求める際にも、円柱の体積や表面積の求め方が大きく関わります。ここでは円柱の体積の求め方を見ていきましょう。 「円柱」の体積を求めてみよう！ 例題 底面の円の半径が 3cm 、高さが 8 cm である円柱の体積を求めなさい。ただし 体積が1570cm³である次の円錐の高さを求めましょう。 （円周率は314とします。） 《円錐の高さの求め方》 円錐の体積＝底面積×円錐の高さ÷3であることから 円錐の高さ＝円錐の体積÷底面積×3で求めることが出来ます。 ここで、底面積＝10×10×314＝314 中学数学「1次方程式」文章題の解き方⑨図形の問題 中学数学「連立方程式」 文章題の解き方①立式のコツ このときの底面abcdから水面までの高さを求めなさい。 基本となる考え方から、円錐の表面積を深く理解するところまで、ポイントを
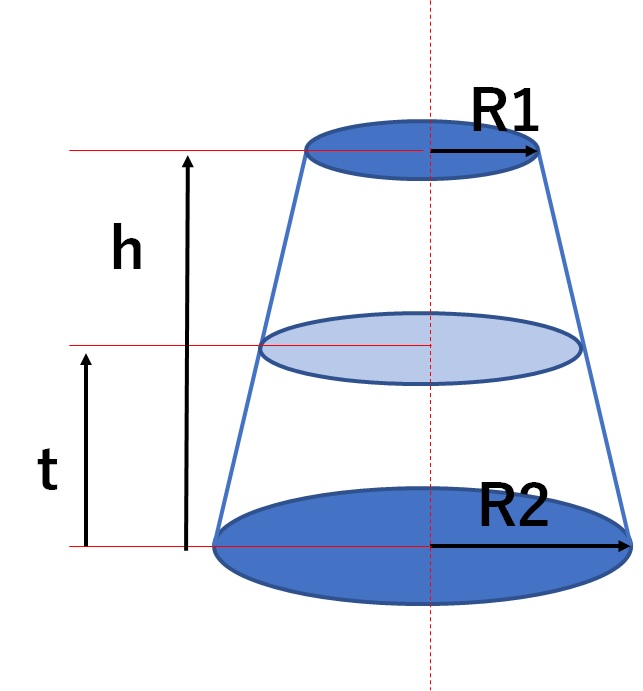
11月26日（火） 角錐の体積の求め方 6年生の算数の授業です。 角錐・円錐の体積の求め方には底面積×高さ÷3という公式があります。 「なぜ、÷3するのか」という疑問を解決するために、四角錐などの立体を組み合わせて考えました。円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学 > 図形 > 円錐台の体積と表面積を計算する公式と証明 最終更新日 図のような円錐台について、 体積は、 V = 1 3 π h ( a 2 a b b 2) 側面積は、 S L = π ( a b) ( a − b) 2 h 2 表面積は、 S錐の体積 = 底面積 × 高さ× 1 3 高さとは>> 頂点から、底面におろした 垂線の長さのこと。 高さ (例) 底面 9cm 2 高さ 10cm 五角錐 体積=9×10÷3=30 正四角錐(底面が正方形) 4cm 6cm 高さ 底面積=4×4=16 体積=16×6÷3=32 高さ8cm 底面の半径 3cm 円錐 底面積=3×3×π=9π 体積=9π×
円錐 高さ 求め方 中学のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |
 高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |
 高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |
「円錐 高さ 求め方 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |
 高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |
 高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |
「円錐 高さ 求め方 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 高校入試対策数学 円錐に関する対策問題 Pikuu | 高校入試対策数学 円錐に関する対策問題 Pikuu | 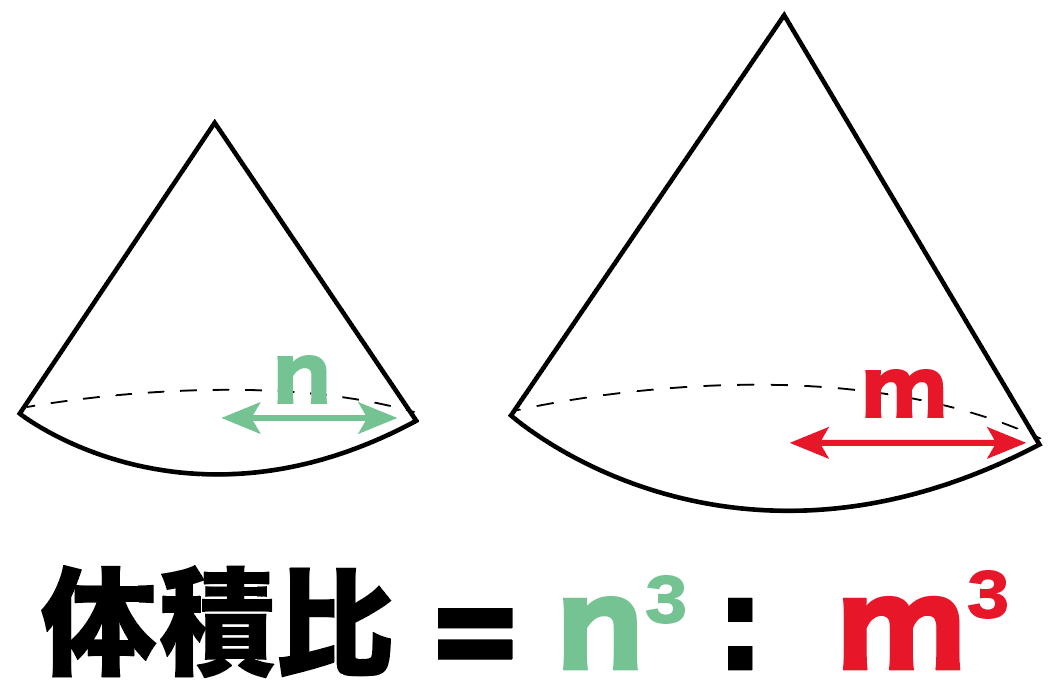 高校入試対策数学 円錐に関する対策問題 Pikuu |
 高校入試対策数学 円錐に関する対策問題 Pikuu | 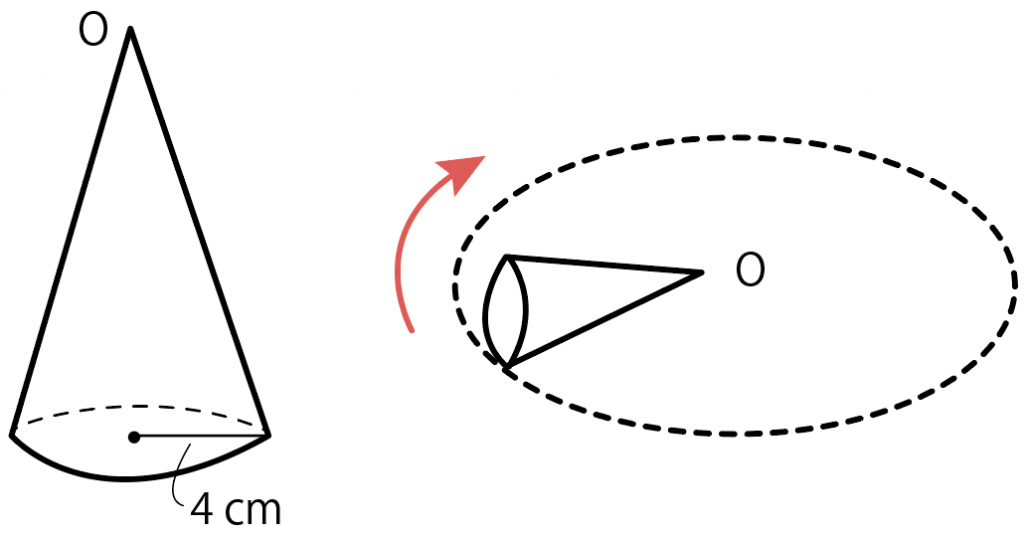 高校入試対策数学 円錐に関する対策問題 Pikuu | 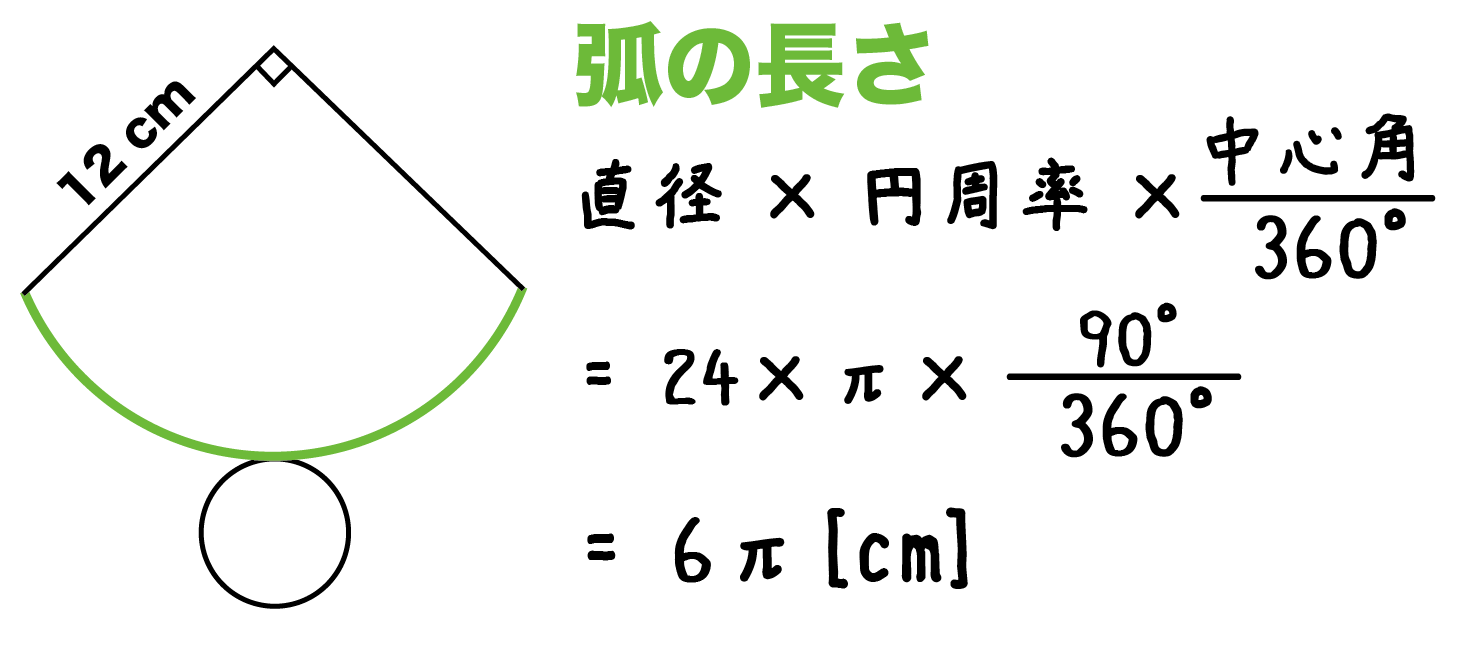 高校入試対策数学 円錐に関する対策問題 Pikuu |
 高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |
「円錐 高さ 求め方 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |
 高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu | 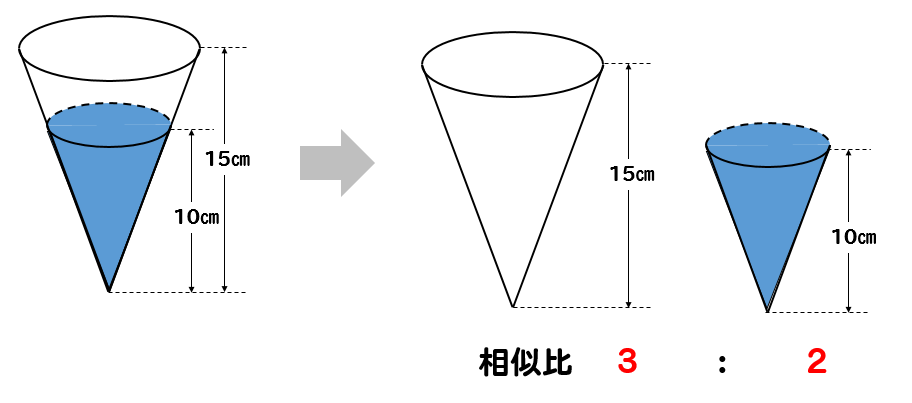 高校入試対策数学 円錐に関する対策問題 Pikuu |
 高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |
「円錐 高さ 求め方 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |
高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu | 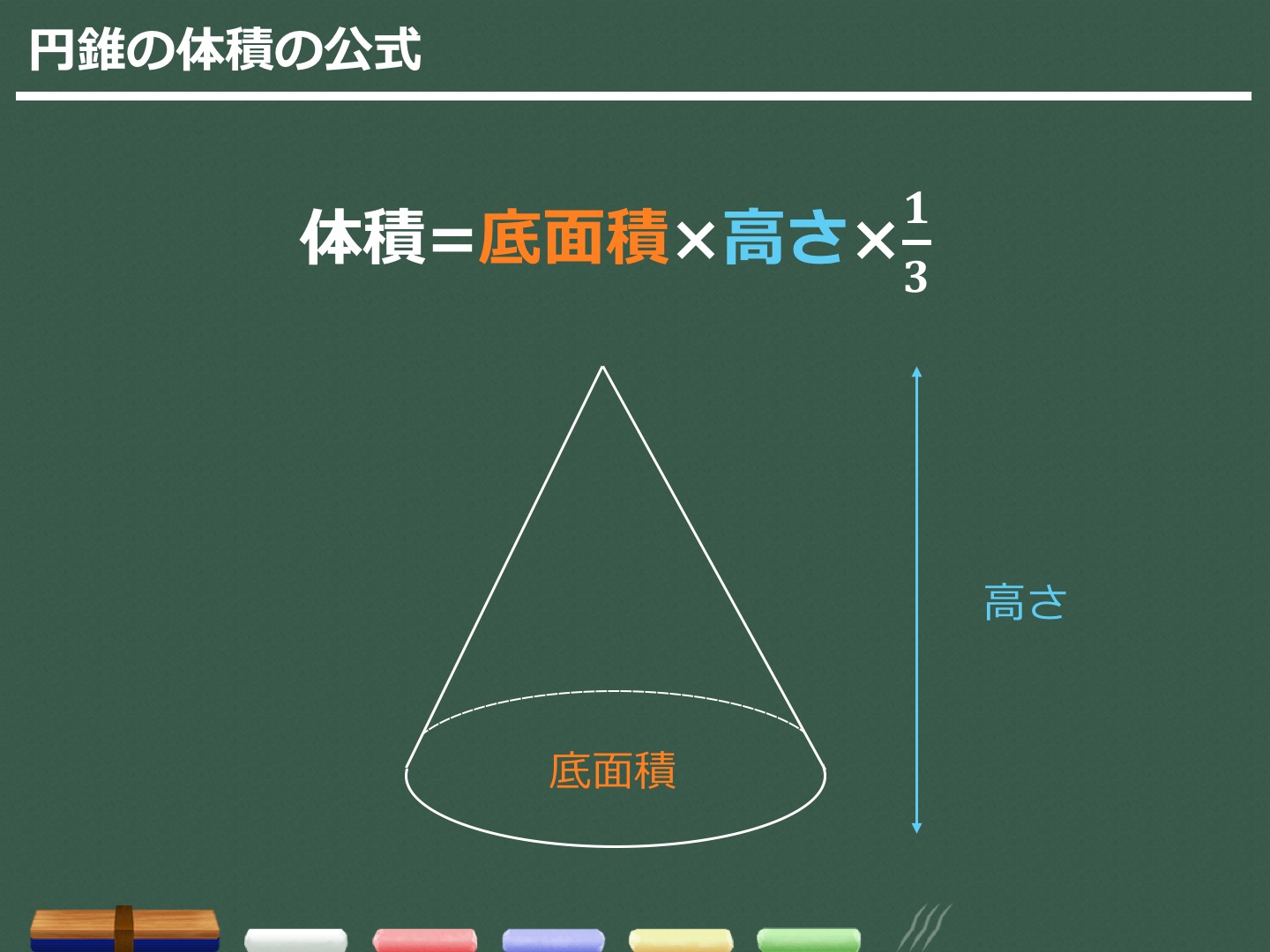 高校入試対策数学 円錐に関する対策問題 Pikuu |
 高校入試対策数学 円錐に関する対策問題 Pikuu | 高校入試対策数学 円錐に関する対策問題 Pikuu | 高校入試対策数学 円錐に関する対策問題 Pikuu |
「円錐 高さ 求め方 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |
 高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |
 高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |
「円錐 高さ 求め方 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |
 高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |
 高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |
「円錐 高さ 求め方 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 高校入試対策数学 円錐に関する対策問題 Pikuu | 高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |
 高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |
高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |
「円錐 高さ 求め方 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |
 高校入試対策数学 円錐に関する対策問題 Pikuu | 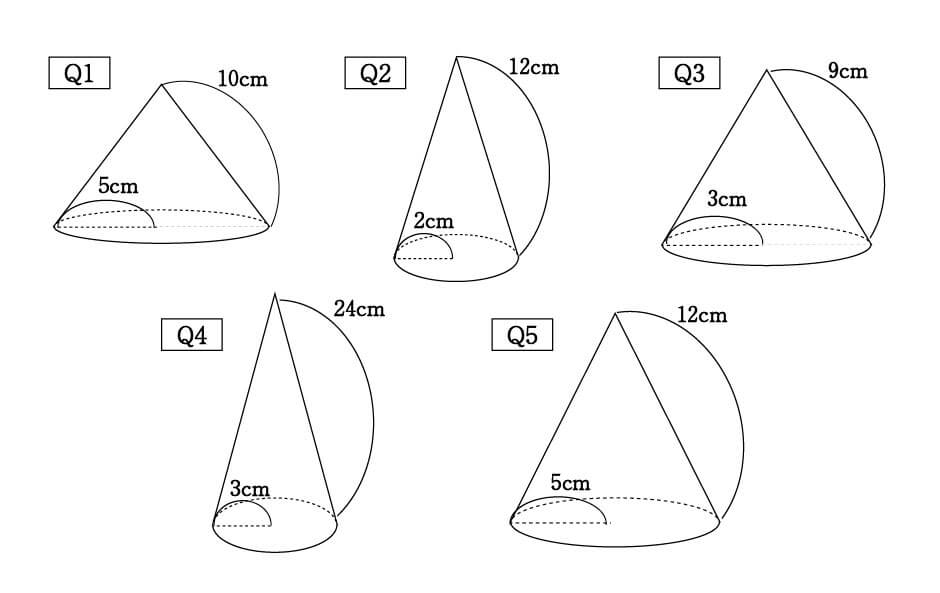 高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |
 高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu | 高校入試対策数学 円錐に関する対策問題 Pikuu |
「円錐 高さ 求め方 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |
 高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |
高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |
「円錐 高さ 求め方 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
 高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |
 高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |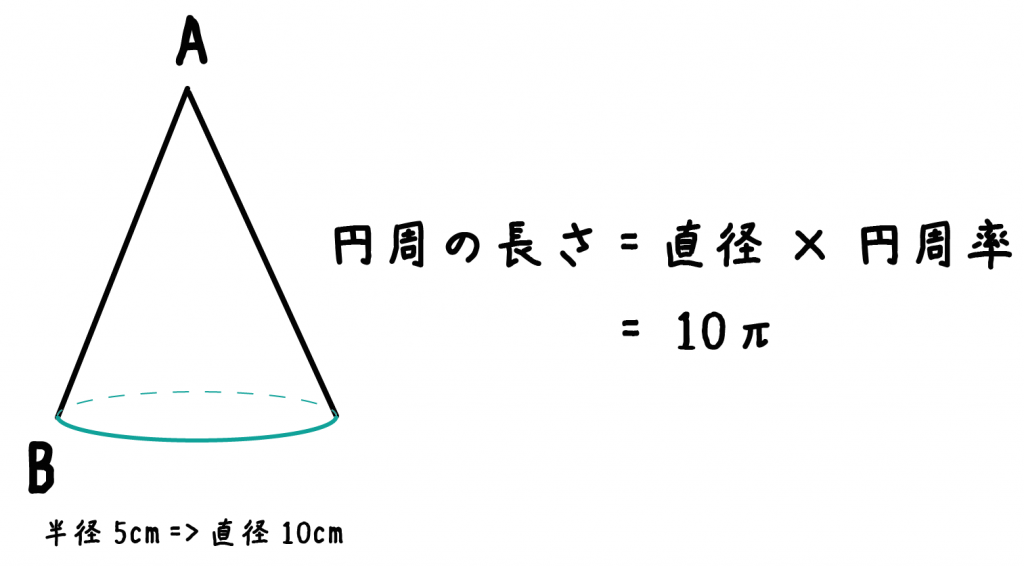
高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |
「円錐 高さ 求め方 中学」の画像ギャラリー、詳細は各画像をクリックしてください。
高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu | 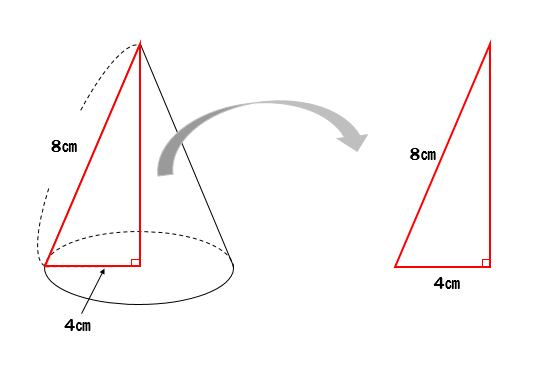 高校入試対策数学 円錐に関する対策問題 Pikuu |
 高校入試対策数学 円錐に関する対策問題 Pikuu |  高校入試対策数学 円錐に関する対策問題 Pikuu |
錐体の体積の求め方：底面積×高さ× →底面積と高さの2つ要素が分かれば体積が分かる． →形が変形しても 底面積と高さが変化しなければ体積も変わらない． ①下図の3つの立体は同じ体積（底面積も高さも同じ） →底面積×高さ× が成り立つ ②回転しTOP > 数学 > 直円錐の公式(体積・側面積・表面積) 直円錐 計算 半径(r) 高さ(h) 体積 \ V = \frac{1}{3} \pi r^2 h \ 側面積 \ F = \pi r \sqrt{ r^2 h^2} \ 表面積 \ S = F \pi r^2 \ EXCELの数式 A B;すごい 円錐 高さ 公式 体積の計算 円柱 製品設計知識 中学数学 円錐の高さの求め方がわかる3ステップ Qikeru 学びを 中
コメント
コメントを投稿